www.michael-buhlmann.de
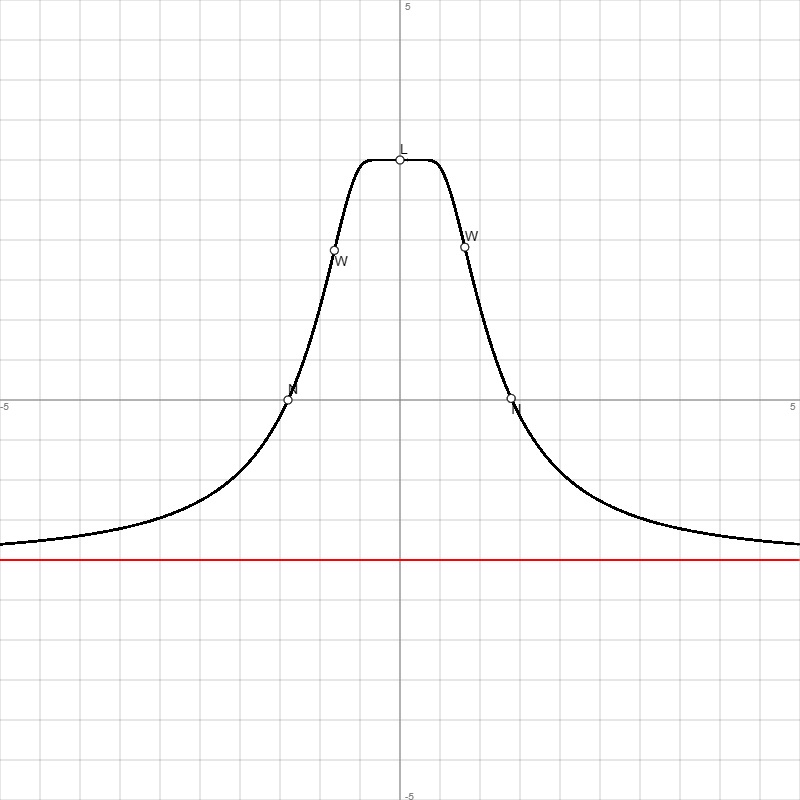
Funktion: f(x) = -5·e-1/x2+3, Df = R\{0}, Wf = (0; 3), reelle Funktion, Funktion achsensymmetrisch zur Senkrechten x = 0, x -> -∞: f(x) -> -2 = y als Grenzkurve, x -> +∞: f(x) -> -2 = y als Grenzkurve ->
| Wertetabelle: | |||||
| x | f(x) | f'(x) | f''(x) | f'''(x) | Besondere Kurvenpunkte |
| -5 | -1.8039 | 0.08 | 0.04 | 0.03 | |
| -4.5 | -1.7591 | 0.1 | 0.07 | 0.06 | |
| -4 | -1.6971 | 0.15 | 0.11 | 0.1 | |
| -3.5 | -1.6081 | 0.21 | 0.17 | 0.19 | |
| -3 | -1.4742 | 0.33 | 0.31 | 0.37 | |
| -2.5 | -1.2607 | 0.55 | 0.58 | 0.81 | |
| -2 | -0.894 | 0.97 | 1.22 | 1.9 | |
| -1.5 | -0.2059 | 1.9 | 2.67 | 4.06 | |
| -1.4 | 0 | 2.19 | 3.09 | 4.31 | Nullstelle N(-1.4|0) |
| -1 | 1.1606 | 3.68 | 3.68 | -7.85 | |
| -0.82 | 1.87 | 4.1 | 0 | -37.24 | Wendepunkt W(-0.82|1.87) |
| -0.5 | 2.9084 | 1.47 | -14.64 | 29.36 | |
| 0 | - | - | - | - | Lücke L(0|3) |
| 0.5 | 2.9084 | -1.47 | -14.64 | -17.68 | |
| 0.81 | 1.911 | -4.1 | 0 | 37.24 | Wendepunkt W(0.82|1.87) |
| 1 | 1.1606 | -3.68 | 3.68 | 6.89 | |
| 1.4 | 0 | -2.22 | 3.14 | -4.31 | Nullstelle N(1.4|0) |
| 1.5 | -0.2059 | -1.9 | 2.67 | -4.02 | |
| 2 | -0.894 | -0.97 | 1.22 | -1.87 | |
| 2.5 | -1.2607 | -0.55 | 0.58 | -0.8 | |
| 3 | -1.4742 | -0.33 | 0.31 | -0.37 | |
| 3.5 | -1.6081 | -0.21 | 0.17 | -0.18 | |
| 4 | -1.6971 | -0.15 | 0.11 | -0.1 | |
| 4.5 | -1.7591 | -0.1 | 0.07 | -0.06 | |
| 5 | -1.8039 | -0.08 | 0.04 | -0.03 | |
| Graph: | |||||
 | |||||
Graph(en) der Asymptote(n), Grenzkurve(n).
Abkürzungen: Df = (maximaler) Definitionsbereich, f(x) = Funktion, f'(x) = 1. Ableitung, f''(x) = 2. Ableitung, f'''(x) = 3. Ableitung, H = Hochpunkt, L = Lücke, N = Nullstelle, P = Polstelle, R = reelle Zahlen, S = Sprungstelle, T = Tiefpunkt, W = Wendepunkt, WS = Sattelpunkt, Wf = Wertebereich, {.} = ein-/mehrelementige Menge, [.; .] = abgeschlossenes Intervall, (.; .) = offenes Intervall, [.; .), (.; .] = halboffenes Intervall, ∞ = unendlich.
Bearbeiter: Michael Buhlmann