Komplexe Zahlen: Wurzeln II
|
Abbildung: |
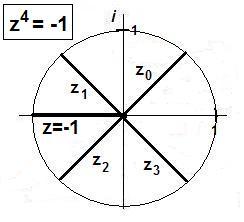 |
Eingabe der kartesischen oder Polarkoordinaten einer komplexer Zahl z und einer natürlichen Zahl n (Dezimalzahlen mit Punkt statt Komma; kartesische Koordinaten: z = a + bi; Polarkoordinaten: z = |z|*eiφ = |z|*(cosφ + i*sinφ), Betrag nichtnegativ, Winkel in Bogenmaß; natürliche Zahl > 1; Rechnung auf fünf Stellen hinter dem Komma genau):